Las psicólogas Blakemore
y Frith (2011) afirman que no existe demasiado sentido buscar una región
cerebral que haga matemáticas, debido a que hay diferentes aspectos que
componen las matemáticas y que implican diferentes regiones. El procesamiento
matemático y el cálculo son capacidades complejas, que implican la
participación de diferentes capacidades cognitivas (verbales, atencionales,
espaciales, memorísticas y ejecutivas), por lo que su sustrato cerebral se
encuentra distribuido en diferentes áreas y/o regiones tanto corticales como
subcorticales, conectadas entre sí formando redes neuronales complejas. Esto
conlleva que puedan surgir dificultades de diversa índole en el procesamiento
numérico (Serra, 2013). La interconexión y múltiples factores del cálculo
también conllevan que la alteración en uno de los componentes cognitivos que
operan en el cálculo, por ejemplo, el lenguaje en el hemisferio izquierdo,
puede llevar a que se vean afectadas la compresión y producción de números.
Esto refleja que existen diferentes sistemas cerebrales implicados en los
distintos aspectos de los números, que se integran para dar coherencia y
sentido como un todo. Lo que sí podemos afirmar es que aún no tenemos el
suficiente conocimiento del funcionamiento de nuestro cerebro matemático. Hasta
el momento, los estudios parecen indicar que diferentes regiones parietales y
prefrontales contribuyen de manera significativa a la función numérica
(Serra-Grabulosa et al., 2010).
El
matemático y doctor en psicología cognitiva Stanislas Dehaene (Cohen y Dehaene, 1994,
1996; Dehaene, 1992, 1997, 2007; Dehaene y Cohen, 1991, 1995, 1997, 2007, 2016;
Dehaene y Mehler, 1992;) es, sin duda, junto con su equipo, el investigador que
ha dado un mayor impulso al estudio de las bases neurocognitivas de las
matemáticas desde finales de los ochenta, tanto mediante el estudio de
pacientes lesionados, como con las modernas técnicas de neuroimagen. En estos y
otros estudios, se asocia el área inferior del lóbulo parietal como la base del
cerebro matemático, ya que esta región se activa durante cualquier actividad
numérica (Cantlon et al., 2006). Las lesiones en esta región pueden dejar al
paciente totalmente incapaz de ejecutar incluso cálculos tan sencillos como 3-1
o 7x8 (Warrington, 1982; Takayama, Sugishita, Akiguchi, Kimura, 1994; Dehaene y
Cohen, 1997). Butterworth (1999) afirma que "está claro que nuestro
Cerebro Matemático está localizado en el lóbulo parietal izquierdo". Pero
el hecho de que la región parietal inferior parezca jugar un papel crucial en
el sentido numérico, no quiere decir que sea la única región cerebral implicada
en el procesamiento numérico.
Dehaene,
Piazza, Pinel y Cohen (2003), identifican el que llaman “circuito del
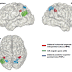
cálculo”, que consta de tres regiones (ver figura):
- Surco intraparietal horizontal superior bilateral (en color rojo en la figura): manipulación de cantidades o sentido numérico (comparación de cantidades numéricas, estimaciones, sustracciones y aproximaciones). Se activa en tareas de cálculo exacto y de cálculo aproximado, de aspectos no simbólicos, como de aspectos simbólicos (Serra, 2013). La activación del surco intraparietal está exclusivamente relacionada con el procesamiento numérico, habiéndose aislado para su comprobación de tareas atencionales, espaciales, del movimiento de los ojos y de los dedos. Se activa con la simple presencia de estímulos numéricos, siempre y cuando estos tengan algún significado cuantitativo, independientemente del formato y tipo del estímulo utilizado, aunque parece ser que existen diferentes grupos de neuronas que responden selectivamente a un formato concreto y otros grupos de neuronas a otro. El surco intraparietal derecho se ocupa de la estimación de magnitudes, mientras el izquierdo de tareas de comparación, tanto de estímulos simbólicos (dígitos) como no simbólicos (ej.: puntos), como de cálculos numéricos. La realización de sumas, restas y multiplicaciones es bilateral, pudiendo verse afectadas si hay lesión en cualquiera de los hemisferios. El surco intraparietal también se encarga de la recuperación de hechos numéricos de la memoria a largo plazo (Serra, 2013).
- Lóbulo parietal posterosuperior bilateral (en color azul en la figura): esta área, relacionada con tareas espaciales y de memoria de trabajo espacial, se asocia con tareas atencionales durante la resolución del cálculo, como por ejemplo, tareas de comparación numérica, cálculo aproximado, sustracción aproximada, contabilización, etc. (Cohen-Kadosh et al., 2011; Kaufmann et al., 2008; Chochon, Cohen, Van de Moortele y Dehaene, 1999). Esta región es claramente multimodal, ya que también se encarga de tareas visoespaciales y de memoria de trabajo espacial (Serra, 2013).
- Circunvolución angular izquierda (en color verde en la figura): región clave en los procesos automáticos y dependientes del lenguaje implicado en la realización de problemas aritméticos. Se encarga de la representación simbólica, mediante palabras o mediante números. Con ello se permite el cálculo exacto (operaciones sencillas exactas que aprendemos de memoria para agilizar el cálculo, como las tablas de multiplicar o las operaciones aritméticas simples con cifras pequeñas menores de 10). Cuando es una multiplicación no automatizada, no interviene el giro angular, sino el surco intraparietal bilateral y áreas prefrontales relacionadas con la atención y la memoria de trabajo. Sustenta la representación cerebral no semántica de las cantidades (procesar el dígito 6 sin asociarlo con una cantidad numérica concreta), (Price y Ansari, 2011; Grabner et al., 2009; Dehaene et al., 1999). Existe una correlación positiva entre la activación del giro angular izquierdo y la competencia matemática (Grabner et al. 2007), al existir mayores automatismos. Por esta razón tiene sentido que a los niños disléxicos les cueste memorizar las tablas de multiplicar, ya que proceso de codificación fonológica depende de la misma región cerebral (Boix et al., 2015). Es el centro de la lesión en el Síndrome de Gerstmann.
A partir de la identificación de estas tres regiones descritas anteriormente, se puede inferir teóricamente la existencia de tres subtipos diferenciados de dificultades en el cálculo:
- Por déficit en el sentido numérico.
- Por alteración en la atención espacial.
- Por dificultades verbales.
Dehaene y Cohen (1995) describen el modelo cognitivo del triple código en el que diferencia tres formatos de representación de las cantidades: el arábigo (5), el verbal (cinco) y un formato abstracto ligado a la magnitud, y que está relacionado con el concepto de numerosidad. Estos autores consideran que el sistema visual (córtex occipito-temporal inferior) del hemisferio izquierdo está asociado con el reconocimiento tanto de cifras arábigas ("7") como de palabras escritas ("siete", mientras que la misma región del hemisferio derecho sólo reconoce las arábigas. En el caso de identificación y producción de palabras habladas, es la región perisilviana del hemisferio izquierdo la que está implicada. Esta región participa también en un circuito cortico-subcortical que comprende también los ganglios basales del hemisferio izquierdo, que se activan en tareas aritméticas rutinarias (tablas de sumar y multiplicar).
Los circuitos dedicados a coordinar las intervenciones de las demás áreas están ubicados posiblemente en el córtex prefrontal, en el córtex cingulado anterior y los circuitos frontosubcorticales, interviniendo en la supervisión de conductas no automatizadas, como son las tareas que requieren planificación, organización, ordenación secuencial, toma de decisiones, corrección de errores, mantenimiento de resultados intermedios y puesta en marcha de la memoria de trabajo. Ante cualquier tarea que requiera resolver un cálculo más complejo se activará esta región cerebral que, al mismo tiempo, realiza una labor de asistencia al giro angular en la recuperación de hechos aritméticos (red frontoparietal) (Jost et al., 2011), identifica y corrige los errores (Menon et al., 2002), y realiza tareas de memoria de trabajo y de focalización de la atención en tareas numéricas. Las regiones prefrontales se activan en mayor medida en los niños pequeños, con menor experiencia y automatización del cálculo, activando mayores recursos atencionales y de meoria de trabajo. Por el contrario, en los niños pequeños se activan en menor medida las regiones parietales. Por tanto, parece que se va dando una especialización parietal. Las áreas prefrontales también se activan más ante operaciones aritméticas incorrectas.
Existen otras regiones cerebrales asociadas al cálculo, como la ínsula anterior izquierda, el cerebelo y el núcleo caudado. Hasta donde se sabe hoy día, la ínsula anterior izquierda y la corteza cerebelosa participan en la recuperación de hechos aritméticos (Zago et al., 2001). La corteza cerebelosa central se asocia con el aprendizaje de secuencias de movimientos realizados con los dedos y con la manipulación de objetos en tres dimensiones (Serra, 2013). Por su parte, el núcleo caudado participa también en el procesamiento numérico y el cálculo, aunque se desconoce con exactitud su función, habiéndose relacionado con cálculos novedosos (no entrenados), y los problemas aritméticos complejos que requieren varios pasos para su resolución (Serra, 2013).
La neurociencia cognitiva contemporánea sólo ha comenzado a investigar los orígenes de los conceptos matemáticos, principalmente a través de estudios de aritmética básica. Yendo más allá, el pensamiento matemático de alto nivel conlleva una activación de una red restringida y consistente de áreas cerebrales. Esta red comprende sitios prefrontales, intraparietales bilaterales, inferotemporales y dorsales. Se activa en todos los dominios matemáticos (análisis, álgebra, topología y geometría) e incluso, trasnsitoriamente, mediante afirmaciones matemáticas sin sentido. Tales problemas activan regiones bilaterales temporales y angulares anteriores. En las tareas matemáticas de alto nivel se hace un uso mínimo de las áreas del lenguaje y en su lugar recluta circuitos inicialmente involucrados en el espacio y el número. Este resultado puede explicar por qué, durante la primera infancia, el conocimiento del número y el espacio predice el logro matemático. En matemáticas, básicamente no se encuentra superposición de la red de respuesta matemática con las áreas activadas por la comprensión de oraciones y el conocimiento semántico en general. Sin embargo, si existe una fuerte superposición y una similitud de la red sensible a las matemáticas con áreas temporales y parietales inferiores activadas durante el cálculo aritmético y el reconocimiento de números (Amalric y Dehaene, 2016). En particular, las regiones temporales inferiores bilaterlaes se han denominado "áreas de forma de números visuales" porque se activan con números arábigos escritos mucho más que con cadenas de letras u otras imágenes (Shum et al., 2013; Hermes et al. 2017) así como por las matemáticas de alto nivel, y por la mera visión de números y fórmulas matemáticas. En consecuencia, se observó una activación reducida a las caras en la circunvolución fusiforme derecha. Estos resultados son análogos a los hallazgos previos sobre alfabetización, lo que demuestra que la adquisición de experiencia en la lectura desplaza las respuestas dela corteza visual ventral izquierda a las letras, compitiendo, reduciendo y desplazando de dicha área la respuesta a las caras (Dehaene et al., 2010; Dundas, Plaut y Behrmann, 2013; Pegado et al., 2014).
 |
Location of preferential responses to
numerals (Shum et al., 2017)
|
<<Una invención cultural, puede
cambiar, por adaptación, la función de un órgano (cerebro) a otra distinta a la
que le dio origen>>
Stanislas Dehaene
(Concepto de reconversión o reciclaje neuronal)
Desde
el punto de vista estructural se ha detectado que las personas con discalculia
disponen de un menor volumen de sustancia gris en áreas que rodean el surco
intraparietal. Además, se han descrito diferencias en la conectividad con
regiones próximas. Igualmente, se ha observado que con los años los sujetos
cambian de dominancia de activación durante las tareas aritméticas,
predominando el hemisferio derecho en los primeros estadios (organización
perceptiva) y, más adelante, el hemisferio izquierdo, con la incorporación del
lenguaje y competencias lingüísticas-simbólicas. Por otro lado, el hemisferio
izquierdo está asociado al procesamiento simbólico y al cálculo exacto.
Mientras que el derecho se identifica con el cálculo aproximado, la estimación
y el subitizing o subitización (en el que predomina el procesamiento
perceptivo) (Boix et al., 2015).
Como vemos, tenemos las primeras aproximaciones a las redes implicadas en las matemáticas, interviniendo multitud de áreas cerebrales, entre las que destaca el surco intraparietal. También se empiezan a conocer los efectos que produce el aprendizaje de las matemáticas en el desplazamiento y reestructuración de las funciones corticales. Sin embargo, aún queda mucho por conocer acerca de una actividad que llega a ser tan sofisticada y compleja, en la que pueden intervenir un gran número de funciones cognitivas, dependiendo de las operaciones matemáticas que llevemos a cabo y de la experiencia y conocimiento que tengamos. En el ámbito de las matemáticas estamos aún lejos del nivel de conocimiento que se tiene en otras tareas como la lectura y la escritura. Avanzar en estos conocimientos nos ayudará a conocer las bases de las dificultades de aprendizaje de las matemáticas, lo que nos permitirá refinar y mejorar las intervenciones que se llevan a cabo.
Como vemos, tenemos las primeras aproximaciones a las redes implicadas en las matemáticas, interviniendo multitud de áreas cerebrales, entre las que destaca el surco intraparietal. También se empiezan a conocer los efectos que produce el aprendizaje de las matemáticas en el desplazamiento y reestructuración de las funciones corticales. Sin embargo, aún queda mucho por conocer acerca de una actividad que llega a ser tan sofisticada y compleja, en la que pueden intervenir un gran número de funciones cognitivas, dependiendo de las operaciones matemáticas que llevemos a cabo y de la experiencia y conocimiento que tengamos. En el ámbito de las matemáticas estamos aún lejos del nivel de conocimiento que se tiene en otras tareas como la lectura y la escritura. Avanzar en estos conocimientos nos ayudará a conocer las bases de las dificultades de aprendizaje de las matemáticas, lo que nos permitirá refinar y mejorar las intervenciones que se llevan a cabo.
Para saber más y mejor:
Amalric, M. y Dehaene, S. (2016) Origins of
the brain networks for advanced mathematics in expert mathematicians.
Proceedings of the National Academy os Sciences of the United States of
America, 113 (18) 4909-4917; https://doi.org/10.1073/pnas.1603205113
Artigas Pallarés, J. (2011) Discalculia. En
J. Artigas-Pallarés y J. Narbona (Coords.) Trastornos del
neurodesarrollo. Barcelona: Viguera.
Blakemore, S. J.; Frith, U. (2015) Cómo aprende el
cerebro. Las claves para la educación. 3ed. Barcelona: Ariel.
Boix, C.; Colomé, R.; López, A. y
Sanguinetti, A. (2015) Trastornos del aprendizaje: dislexia, disgrafía y
discalculia. En A. Enseñat; T. Roig y A. García (Coords.) Neuropsicología
pediátrica. Madrid: Síntesis. pp. 101-118.
Butterworth, B. (1999) The Mathematical
Brain. London: McMillan.
Cantlon, J.F.; Brannon, E.M.; Carter, E.J.;
Pelphrey, K.A. (2006) Functional imaging of numerical processing in adults and
4-y-old children. PLoS Biology, 4(5):e125. doi:
10.1371/journal.pbio.0040125
Cohen, L. y Dehaene, S. (1994). Amnesia for
arithmetic facts: A single case study. Brain and Language, 47, 214-232.
Cohen, L. y Dehaene, S. (1996). Cerebral
networks for number processing: Evidence from a case of posterior callosal
lesion. NeuroCase, 2, 155-174.
Cohen-Kadosh; R.; Bahrami, B.; Walsh, V.;
Butterworth, B.; Popescu, T.; Price, C.J. (2011) Specialization in the human
brain: the case of numbers. Frontiers of Human
Neuroscience, 5, 62.
Chochon, F.; Cohen, L.; Van de Moortele,
P.F.; Dehaene, S. (1999) Differential contributions of the left and right
inferior parietal lobules to number processing. Journal of Cognitive
Neuroscience, 11, 617-630.
Dehaene, S. (1992). Varieties of numerical
abilities. Cognition,
44, 1-42.
Dehaene, S. (1997). The Number Sense: How
the Mind Creates Mathematics. New York: Oxford University Press.
Dehaene, S. (2007) The number sense. How
the Mind Creates Mathematics. New York: Oxford University Press, 1997;
Cambridge (UK): Penguin press.
Dehaene, S. (2016) El cerebro matemático.
Buenos Aires: Siglo XXI.
Dehaene, S. y Cohen, L. (1991). Two mental
calculation systems: A case study of severe acalculia with preserved
approximation. Neuropsychologia,
29, 1045-1074.
Dehaene, S. y Cohen, L. (1995). Towards an
anatomical and functional model of number processing. Mathematical
Cognition, 1, 83-120.
Dehaene, S. y Cohen, L. (1997). Cerebral
pathways for calculation: double dissociation between rote verbal and
quantitative knowledge of arithmetic. Cortex, 33,
219-250.
Dehaene, S. y Mehler, J. (1992).
Cross-linguistic regularities in the frequency of number words. Cognition, 43,
1-29.
Dehaene, S.; Piazza, M.; Pinel, P.; Cohen,
L. (2003) Three parietal circuits for number processing. Cognitive
Neuropsychology, 20, 487-506.
Dehaene, S; Pegado, F.; Braga, L.W.;
Ventura, P.; Filho, G.N.; Jobert, A. (2010) How Learning to Read Changes the
Cortical Networks for Vision and Language. Science, 330,
6009, 1359-1364.
Dehaene, S.; Spelke, E.; Pinel, P.;
Stanescu, R.; Tsivkin, S. (1999) Sources of mathematical thinking behavorial
and brain-imaging evidence. Science, 284,
970-974.
Dundas, E.M.; Plaut, D.C.; Behrmann, M.
(2013) The joint development of hemispheric lateralization for words and faces.
Journal of
Experimental Psychology General, 142(2):348–358.
Grabner, R.H.; Ansari, D.; Reishofer, G.;
Stern, E.; Ebner, F.; Neuper, C. (2007) Individual differences in
mathematical competence predict parietal brain activation during mental
calculation. Neuroimage,
38, 346-356.
Grabner, R.H.; Ischebeck, A.; Reishofer,
G.; Koschutnig, K.; Delazer, M.; Ebner, F.; Neuper, C. (2009) Fact learning in
complex arithmetic and figural-spatial tasks: the rol of the anguar gyrus and
its relation to mathematical competence. Human Brain Mapping,
30, 2936-295.
Hermes, D.; Rangarajan, V.; Foster, B.L.;
King, J.R.; Kasikci, I.; Miller, K.J.; Parvizi, J. (2017) Electrophysiological
Responses in the Ventral Temporal Cortex During Reading of Numerals and
Calculation. Cerebral
Cortex, 27, 1: 567–575.
Jost, K.; Khader, P.H.; Burke, M.; Bien,
S.; Rösler, F. (2011) Frontal and parietal contributions to arithmetic fact
retrieval: a parametric analysis of the problema-size effect. Human Brain Mapping,
32, 51-59.
Kaufmann, L.; Vogel, S.E.; Wood, G.;
Kremser, C.; Schocke, M; Zimmerhackl, L.B.; Koten, J.W. (2008) A developmental
fMRI study of nonsymbolic numerical and spatial processing, Cortex, 44 (4),
376-385.
Menon, V.; Mackenzie, K.; Rivera, S.M.;
Reiss, A.L. (2002) Prefrontal cortex involvement in processing in correct
arithmetic equations: evidence from event-related fMRI. Human Brain Mapping,
16, 119-130.
Pegado, F.; Comerlato, E.; Ventura, F.;
Jobert, A.; Nakamura, K.; Buiatti, M.; Ventura, P.; Dehaene-Lambertz, G.;
Kolinsky, R.; Morais, J.; Braga, L.W.; Cohen, L.; Dehaene, S. (2014) Timing the
impact of literacy on visual processing. Proceedings of
National Academy of Science, 111(49):E5233–E5242.
Price, G.R.; Ansari, D. (2011) Symbol
processing in the left angular gyrus: evidence from event-related fMRI. Human Brain Mapping,
16, 119-130.
Serra, J.M. (2013) Representación numérica.
En D. Redolar (coord.) Neurociencia
cognitiva. Madrid: Editorial Médica Panamericana.
Shum, J.; Hermes, D; Foster, B.L.,
Dastjerdi, M.; Rangarajan, V.; Winawer, J.; Miller, K.J.; Parvizi, J. (2013) A
brain area for visual numerals. Journal of
Neuroscience 33(16):6709–6715.
Takayama, Y.; Sugishita, M.; Akiguchi, I.,
y Kimura, J. (1994). Isolated acalculia due to left parietal lesion. Archives of Neurology,
51, 286-291.
Warrington, E. (1982). The fractionation of
arithmetical skills: A single case study. Quarterly Journal of
Experimental Psychology, 34A, 31-51.
Zago, L.; Pesenti, M.; Meller, E.;
Crivello, F.; Mazoyer, B.; Tzourio-Mazoyer, N. (2001) Neural correlates of
simple and complex mental calculation. Neuroimage, 13,
314-327.















0 comments